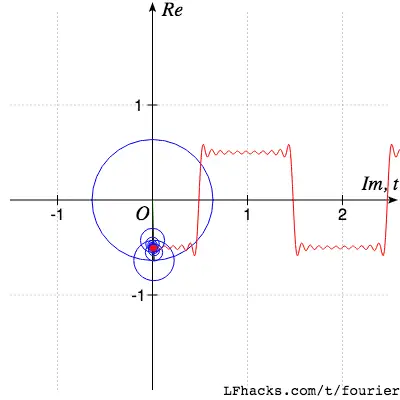
傅里叶变换看似复杂,但今天我们会用最简单的方法来介绍这个强大的工具。不管你是小学生还是对数学感到困难,都能轻松理解。它不仅解释了原理,还配有大量动画和手动操作,便于理解,确实非常出色。
傅里叶变换初识
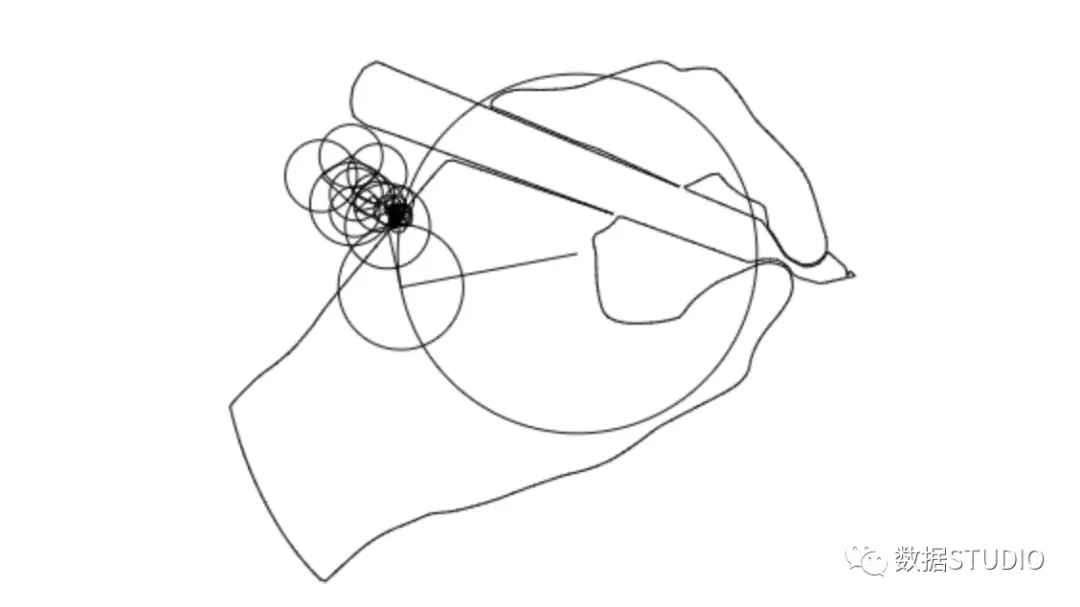
傅里叶变换将复杂的波形拆解为单一的正弦波。举例来说,一个看似复杂的波形,通过傅里叶变换,我们就能了解它是由哪些正弦波组合而成。这并非空洞的理论,它在众多实际场景中都能派上用场。有些波形看似与正弦波毫无关联,但依然可以通过这种方法进行分析。

掌握傅里叶变换的知识,能促进对波形间相互关系的深入研究。比如,面对那些不规则的波形,以前我们难以发现它们的规律性。而现在,借助傅里叶变换,我们能够从构成波形的正弦波入手,去理解和分析这些波形。
手动加深理解

傅里叶变换的这种解释非常难得,因为它允许我们亲手操作。我们能够亲手绘制图形,接着移动滑块来体验变化。比如,在展示方波时,理论上需要无穷多个正弦波才能完美呈现。然而,在实际操作中,移动滑块时你会发现,仅仅前几个正弦波的叠加就能带来显著的变化。
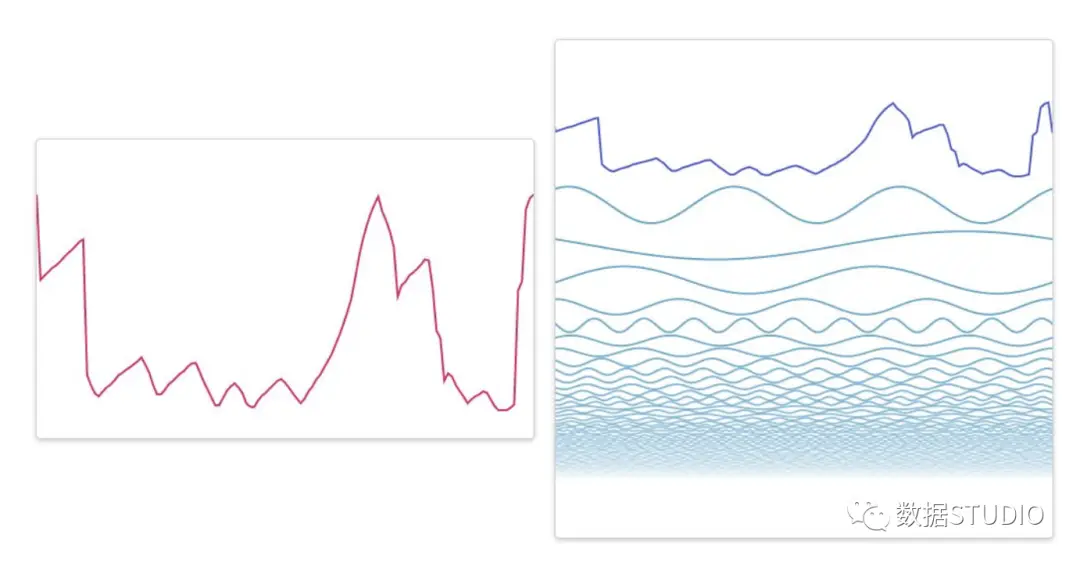
逐渐添加更多的小正弦波,形成的波形会逐渐逼近您所绘制的原始波形。同时,通过调整中间的滑动条,就能获得与原始图形极为相似的波形。这对我们深入理解傅里叶变换的构成原理大有裨益。每一次操作,每一次变动,都直观地揭示了组成的过程。
音频方面的应用
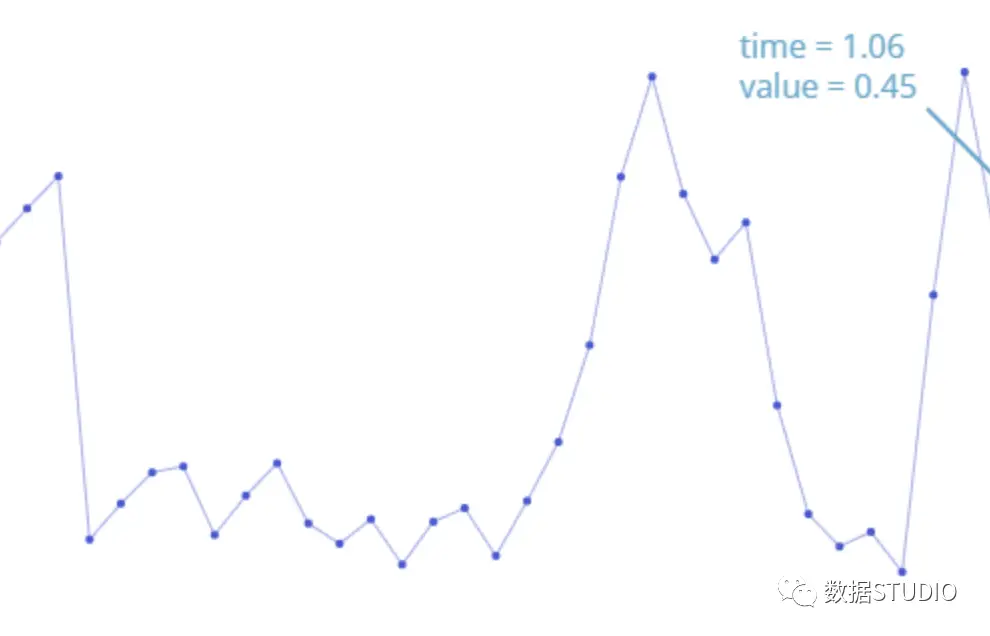
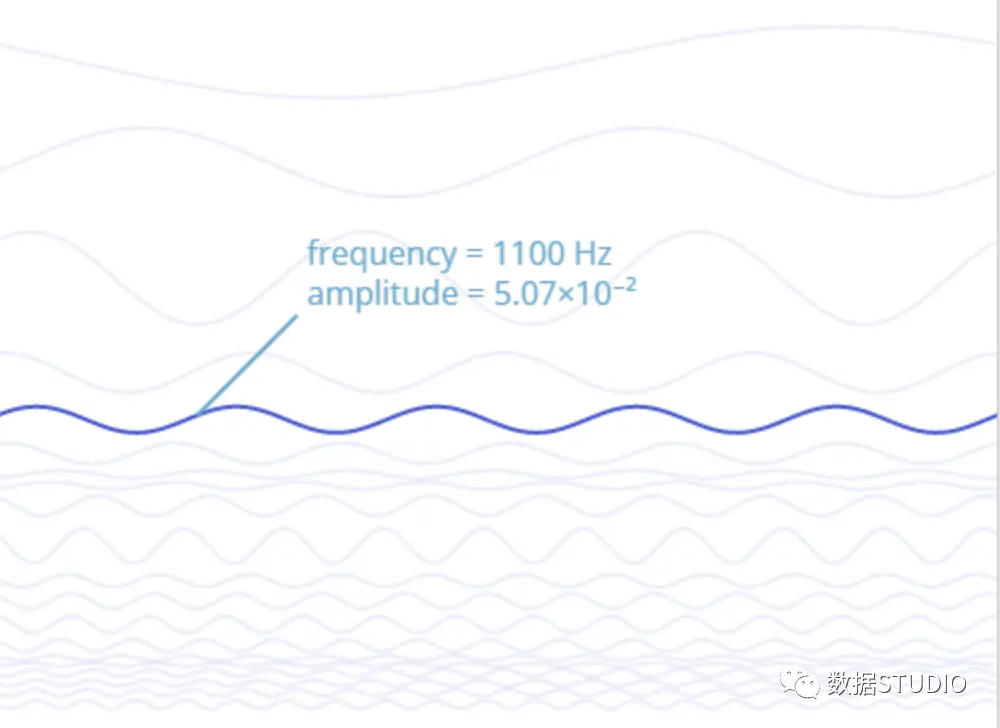
傅里叶变换在音频处理中非常关键。音频可以被看作是由多个正弦波构成的。运用傅里叶变换,我们可以将音频中的关键部分提取出来。经过重新组合,这些部分可以恢复出与原始声音非常相似的波形。这种方法在音频处理领域有着广泛的应用。
在制作音乐时,若需提升音质或减小文件大小,可运用此方法。此法可保留音乐中的关键部分,同时删减掉一些非必要内容。此外,众多音频编辑工具也已普遍采用这一原理对音频资料进行编辑。
2D与3D中的傅里叶变换

2D波的傅里叶变换有其独特性。在变换过程中,会舍弃那些“复杂”的部分,最终呈现出正弦波。相比之下,3D变换则截然不同,它能创造出许多有趣的作品。借助3D正弦波,我们可以制作出形态各异的造型。
傅里叶变换在从二维到三维的演变中展现了其广泛的应用领域和极强的适应性。在二维领域,它主要涉及波形的拆分与重组;而进入三维,则拓展了更多创意与观赏价值。这种转变同样揭示了其多样化和巨大的发展潜力。
图像原理相关
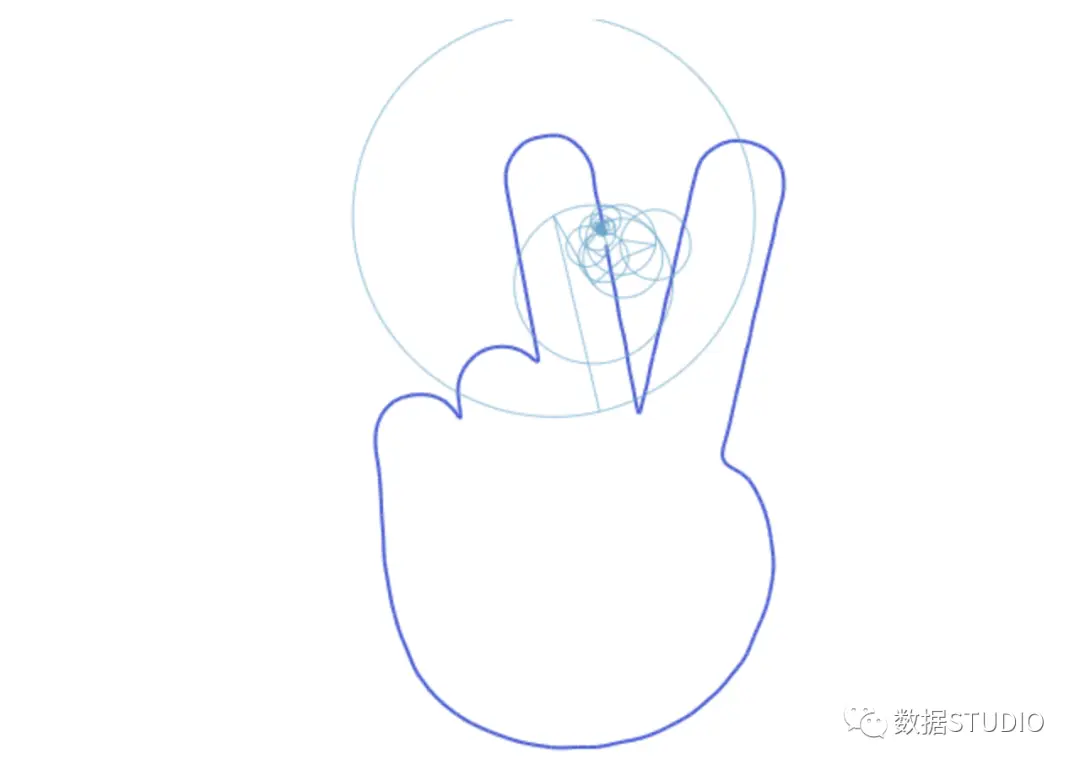
图像处理中,傅里叶变换运用了其独有的理论。我们需要选取一种特定的波形——正弦波——来描绘图像。具体来说,可以将若干个细小的图像片段视作正弦波,例如采用黑白相间的条纹图像。对这些小图像的明暗度进行调节并累加,便能够合成出任何所需的图像。

以JPEG图像为例,其原理大致如此,虽然细节略有不同。这种原理为图像处理和合成开辟了独特的方法,同时也有利于深入认识图像的结构,并优化图像的存储设计。

傅里叶变换的强大之处
傅里叶变换是一项极为有力的技术,其核心在于将事物分解为不同频率的成分。在众多科学研究和实际应用中,这种方法在分析事物频率组成方面发挥着不可替代的作用。无论是研究物理中的波动,还是在计算机技术中处理数据,这种方法都至关重要。
傅里叶变换如今已被众人熟知,那么,你们能否想象,它还能被用于哪些新颖的领域?期待大家分享你们的见解,点赞或转发此文,让更多的人认识到这一有力工具。
版权说明:本文章为昆明鱼豆网所有,未经允许不得转载。